[译]用Ryser算法计算矩阵的永久性

原文地址：https://www.codeproject.com/Articles/21282/Compute-Permanent-of-a-Matrix-with-Ryser-s-Algorit

原文作者：hanzzoid

译文由本站 robot-v1.0 翻译

前言

A quick introduction to permanents and an implementation of a variant of Ryser’s formula

快速介绍永久物以及Ryser公式的变体的实现

介绍(Introduction)

本文介绍了矩阵的永久性(作为将矩阵映射到实数的函数),尤其是介绍了Ryser公式的直接实现,以计算确切的永久性(This article introduces the permanent of a matrix (as a function mapping matrices to real numbers) and in particular a straightforward implementation of Ryser’s formula to compute the exact permanent in) O(n*2^n) .(.)

虽然永久物的定义与行列式类似,但行列式在(Although permanents are defined similarly to the determinant, the latter being computable in) T(n³) (请参阅我在CodeProject上的CSML项目),到目前为止,还没有用于永久计算的多项式算法.((see my CSML project on CodeProject), no polynomial algorithm for permanent computation is known so far.)

此外,计算0-1矩阵的永久性(Furthermore, the computation of a permanent of a 0-1-matrix) A 是#P-complete,并且针对永久物的多项式算法将特别暗示(is #P-complete, and a polynomial algorithm for permanents would particularly imply)P =NP(P = NP).但是,近似值很可能会出现:“当(. However, approximation is well possible: “When the entries of) A 如果为非负数,则可以在概率多项式时间内近似计算出永久物,误差最大为(are nonnegative, the permanent can be computed approximately in probabilistic polynomial time, up to an error of) eM ,在哪里(, where) M 是永久物的价值,(is the value of the permanent and) e > 0 是任意的."(请参阅(is arbitrary.” (See) 维基文章(Wiki article) )(.))

定义(Definition)

让(Let)

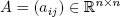成为真实(be a real) n 通过(by) n 矩阵,则永久性定义为(matrix, then the permanent is defined by)

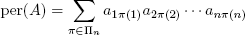(莱布尼兹的公式),其中((Leibniz’s formula), where)

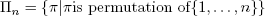例如,考虑(For instance, consider the) n 通过(by) n 1矩阵(1-matrix) U (所有条目都是一个),然后我们会收到((all entries are ones), then we receive) per(U) = n! -为什么呢？有(– why? There are) n! 的排列(permutations of) {1,...,n} ,莱布尼兹公式中的每个置换乘积都等于1.(, and each permutated product in Leibniz’s formula is equal to one.)

莱布尼兹公式的复杂性:(Complexity of Leibniz’s formula:) (n-1)*(n!) 拖鞋,这是超指数的.(flops, which is super-exponential.)

可悲的是,没有关于永久物是什么的几何解释(行列式可以认为是永久物(Sadly, there is no geometric interpretation of what a permanent is (determinants can be considered an) n -体积);它的用途主要是在组合学和图论中:永久性是对二分图中完全匹配数的计数((-dimensional volume); its use is mainly in combinatorics and graph theory: The permanent is a count for the number of perfect matchings in a bipartite graph () ibd(ibd) ).().)

此外,存在类似于行列式拉普拉斯算子的递归算法.您可以通过(Moreover, there is a recursive algorithm similar to the Laplacian development of the determinant. You can develop by the) i 第排(-th row)

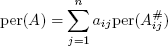或通过(or by the) j 第列(-th column)

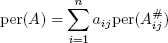在哪里(where the) i-j -次要(-minor of) A 由定义(is defined by)

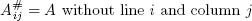该算法仍然是超指数的,但是非常适合手动计算非常小的矩阵的永久性.(This algorithm is still super-exponential, but it is well suited to calculate permanents of very small matrices by hand.)

雷塞尔公式(Ryser’s Formula)

用于计算永久物的最快已知精确算法归功于Ryser:(The fastest known exact algorithm for the computation of the permanent is due to Ryser:)

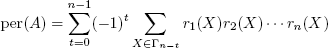哪里(where)

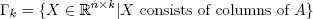是所有的集合(is the set of all) n 通过(by) k 的子矩阵(submatrices of) A 和(, and)

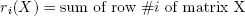是个(is the) i 的第三行总和(-th row sum of) X .理想情况下,Ryser的算法需要(. Ideally, Ryser’s algorithm needs) (n-1)(2^n - 1) 拖鞋这里介绍的实现在(flops; the implementation presented here runs in) O((n^2)(2^n)) .(.)

代码(The Code)

首先,我们需要将十进制转换为带有附加元素(最后一个)的二进制数组,以保存数组中的位数:(At first, we need to transform a decimal to a binary array with an additional element (the last one) saving the number of ones in the array:)

inline int* dec2binarr(long n, int dim)
{
    // note: res[dim] will save the sum res[0]+...+res[dim-1]
    int* res = (int*)calloc(dim + 1, sizeof(int));   
    int pos = dim - 1;

    // note: this will crash if dim < log_2(n)...
    while (n > 0)
    {
        res[pos] = n % 2;
        res[dim] += res[pos];
        n = n / 2; // integer division        
        pos--;
    }

    return res;
}

这里是实际的算法:(Here comes the actual algorithm:)

long per(int* A, int n) // expects n by n matrix encoded as vector
{
    long sum = 0;
    long rowsumprod, rowsum;
    int* chi = new int[n + 1];    
    double C = (double)pow((double)2, n); 

    // loop all 2^n submatrices of A
    for (int k = 1; k < C; k++)
    {
        rowsumprod = 1;
        chi = dec2binarr(k, n); // characteristic vector        

        // loop columns of submatrix #k
        for (int m = 0; m < n; m++)
        {
            rowsum = 0;

            // loop rows and compute rowsum
            for (int p = 0; p < n; p++)
                rowsum += chi[p] * A[m * n + p];
        
            // update product of rowsums
            rowsumprod *= rowsum;    
        
            // (optional -- use for sparse matrices)
            // if (rowsumprod == 0) break;    
        }        
        
        sum += (long)pow((double)-1, n - chi[n]) * rowsumprod;        
    }    

    return sum;
} 

笔记(Notes)

• 通过使用特征向量选择子矩阵(The submatrices are chosen by use of a characteristic vector) chi (仅考虑列,其中((only the columns are considered, where) chi[p] == 1 ).要检索(). To retrieve the) `` 根据Ryser的公式,我们需要保存数字(from Ryser’s formula, we need to save the number) n-t ,就像在(, as is done in) chi[n] .然后我们得到(. Then we get) t = n - chi[n] .(.)
• 矩阵参数(The matrix parameter) A 期望是一维整数数组-矩阵是按行还是按列编码？ -没关系.在行切换和列切换下,永久变量是不变的,它是(is expected to be a one-dimensional integer array – should the matrix be encoded row-wise or column-wise? – It doesn’t matter. The permanent is invariant under row-switching and column-switching, and it is) .(.)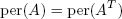
• 进一步的增强:如果有的话(Further enhancements: If any) rowsum 等于零,整个(equals zero, the entire) rowsumprod 变为零,因此(becomes zero, and thus the) m -循环可能会中断.由于if语句与整数运算相比相对昂贵,因此这可能仅节省稀疏矩阵(大多数条目为零)的时间.(-loop can be broken. Since if-statements are relatively expensive compared to integer operations, this might save time only for sparse matrices (where most entries are zeros).)
• 如果有人找到了针对永久物的多项式算法,他将变得富有而闻名(至少在计算机科学界如此).(If anyone finds a polynomial algorithm for permanents, he will get rich and famous (at least in the computer science world).)

历史(History)

• 13(13)日(th)2007年11月:初始职位(November, 2007: Initial post)

许可

本文以及所有相关的源代码和文件均已获得The Code Project Open License (CPOL)的许可。