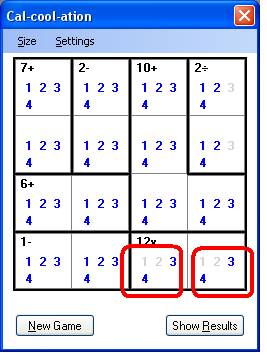
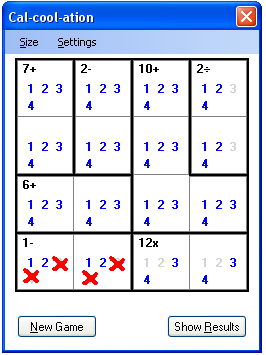
Calcoolation:数学益智棋盘游戏(译文)
By robot-v1.0
本文链接 https://www.kyfws.com/games/calcoolation-a-math-puzzle-board-game-zh/
版权声明 本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
- 8 分钟阅读 - 3797 个词 阅读量 0Calcoolation:数学益智棋盘游戏(译文)
原文地址:https://www.codeproject.com/Articles/38454/Calcoolation-A-Math-Puzzle-Board-Game
原文作者:Marcelo Ricardo de Oliveira
译文由本站 robot-v1.0 翻译
前言
Demo for a math puzzle board game
数学益智桌游演示
- 下载源代码26.64 KB(Download source code - 26.64 KB)
- 下载VS2005源代码-23.93 KB(Download VS2005 source code - 23.93 KB)
- 下载二进制文件-36.57 KB(Download Binaries - 36.57 KB)
介绍(Introduction)
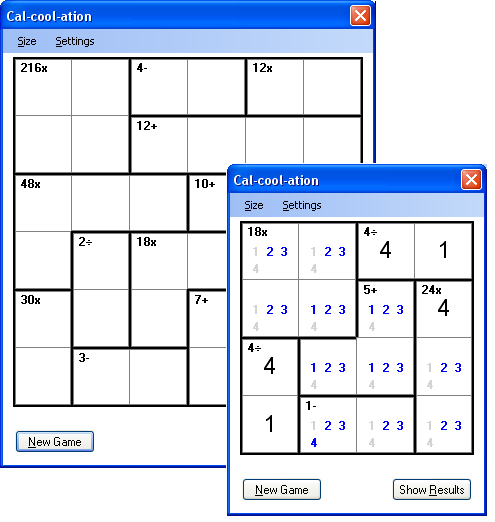
" Calcoolation"是一款益智游戏,最初看起来像是流行的Sudoku.就像数独一样,您有一个N x N矩阵,其中1到N的数字必须放在每一列和每一行中,而不能重复.区别在于,存在名为"笼"的单元格块,其中涉及单元格中数字的特定操作必须满足笼中显示的特定结果.(“Calcoolation” is a puzzle game that at first looks like the popular Sudoku. Just like in Sudoku, you have an N x N matrix, where the digits 1 through N must be placed in each column and in each row without repetition. The difference lies in the fact that there are blocks of cells, named “cages”, where specific operations involving the numbers in the cells must satisfy the specific result displayed in the cage.)
背景(Background)
这款游戏是由日本老师宫本哲也(Tetsuya Miyamoto)于2004年发明的,名称为" KenKen"(Ken是日语中"聪明"的意思),尽管我只是在今年年初才意识到这一点.我对它印象深刻(“困惑”),然后决定用C#开发游戏.(This game was invented by the Japanese teacher Tetsuya Miyamoto in 2004, under the name “KenKen” (Ken is the Japanese word for “cleverness”), although I only became aware of it in the beginning of this year. I got very impressed (“puzzled”) by it, and then decided to develop the game in C#.) 最具挑战性的部分是找到正确的策略来选择随机数,而不必在行和列中重复.我决定使用"裸体对/裸体三胞胎"策略,该策略是我从一些致力于数独求解的站点中借鉴的.我将在本文稍后讨论裸对.(The most challenging part was to discover the correct strategy to pick the random numbers without repetitions in columns and rows. I decided to use the “Naked Pairs/Naked Triplets” strategy, which I borrowed from some sites dedicated to Sudoku solving. I’ll discuss Naked Pairs later on in this article.) 选择所有数字后,我仍然不得不随机创建"笼子".笼子是板上连续的电池组.我是通过从左上角/左上角开始随机选择成对的单元格来实现的.因此,最初的笼子有两个单元,但是当一个随机的笼子单元叠加另一个笼子单元时,这些笼子会合并,因此我们可以有3件式和4件式的笼子.(After picking all the numbers, I still had to randomly create the “cages”. Cages are sets of contiguous cells in the board. I did this by randomly selecting pairs of cells in random directions, beginning from the top/left corner. Thus, initially the cages had two cells, but when a random cage cell superposes another cage cell, those cages are merged, so we could have 3-pieces and 4-pieces cages.)
代码(The Code)
该代码分为两层:Core和WinUI.在WinUI层中,我们具有Windows Forms表示逻辑.这是一个非常简单的用户界面,旨在简化播放器的使用寿命.这里的重要说明是我创建了一个用户控件("(The code is divided into two layers: Core and WinUI. In the WinUI layer, we have the Windows Forms presentation logic. It’s a very simple user interface, intended to make the player life easier. The important note here is that I created a user control (") CellBox “)来保存单元格数据,功能和事件.在Windows窗体中,用户控件是用于在UI端分离问题的有用工具.(") to hold the cell data, functionality, and events. In Windows Forms, user controls are useful tools for separation of concerns on the UI side.)
核心层完成了大部分艰苦的工作.它由代表游戏中三个主要实体的类组成:(The Core layer does most of the hard work. It’s composed of classes that represent the three main entities in the game: the) Board ,(, the) Cage 和(, and the) Cell .只可以有一个人(. There can be only one) Board 在游戏中(这就是我决定使用Singleton模式的原因).默认值(in the game (that’s why I decided to use the Singleton pattern). The default) Board 具有预定义的尺寸4x4(以后可以由用户更改).板上的每个位置都由一个单元格保持(即,单元格数=size²).在板子内部,单元也被分成称为”(has the predefined dimension 4x4 (which can be changed later by the user). Each position in the board is held by a cell (that is, cell count = size²). Inside the board, the cells are also arranged in pieces called “) Cages “(很像传统的难题).(” (much like a traditional puzzle).)
我认为值得一提的是与随机数选择,随机笼形成和游戏完整测试有关的代码.(The pieces of code that I think worth mentioning are those related to random number picking, random cage formation, and game complete testing.)
随机数选择(Random Number Picking)
有关随机数选择,请参见(For random number picking, see the) GenerateNumbers() 方法:(method:)
private void GenerateNumbers()
{
ResetBoard();
Random rnd = new Random();
string number = "0";
int minSize = size;
int maxSize = 0;
bool someSolved = true;
while (someSolved)
{
someSolved = false;
//Search for naked pairs in rows
if (!someSolved)
{
//code removed for better visibility
}
//Search for naked pairs in columns
if (!someSolved)
{
//code removed for better visibility
}
//Search for naked triplets in rows
for (int row = 0; row < size; row++)
{
//code removed for better visibility
}
//Search for cells with a unique solution possible
for (int row = 0; row < size; row++)
{
//code removed for better visibility
}
//Random selection
if (!someSolved)
{
//code removed for better visibility
}
}
}
请注意,根据上面的代码,裸对在开始时就已解析.然后,裸露的三胞胎,然后是具有唯一解的单元格,然后是随机选择.这样做是为了避免回溯.(Notice that, according to the code above, the naked pairs are resolved in the beginning. Then, the naked triplets, and then the cells with a unique solution, and then the random selection. This is done so to avoid backtracking.)
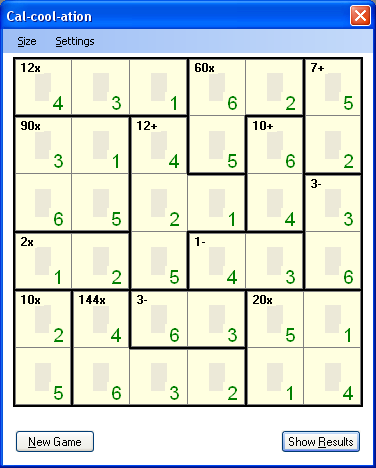
结果,我们现在有了一个有效的板,可以使用:(As a result, we now have a valid board, ready to be used:)
随机笼形成(Random Cage Formation)
接下来的重要步骤是随机创建笼子,这是(The next important step is to randomly create the cages, and here is the) GenerateCages 方法:(method:)
private void GenerateCages()
{
cages = new List<Cage>();
bool success = false;
int orientation = 0;
int c2 = 0;
int r2 = 0;
Random rnd = new Random();
for (int r = 0; r < size; r++)
{
for (int c = 0; c < size; c++)
{
if (matrix[c, r].Cage == null)
{
success = false;
while (!success)
{
orientation = rnd.Next(1, 5);
switch (orientation)
{
case 1: // W
c2 = c - 1;
r2 = r;
break;
case 2: // E
c2 = c + 1;
r2 = r;
break;
case 3: // N
c2 = c;
r2 = r - 1;
break;
case 4: // S
c2 = c;
r2 = r + 1;
break;
}
if (c2 >= 0 && c2 < size && r2 >= 0 && r2 < size)
{
Cage cage = matrix[c2, r2].Cage;
if (cage == null)
{
cage = new Cage();
cage.CellList.Add(matrix[c2, r2]);
matrix[c2, r2].Cage = cage;
}
else
{
if (cage.CellList.Count > 3 && (c != size - 1 || r != size - 1))
{
continue;
}
}
cage.CellList.Add(matrix[c, r]);
matrix[c, r].Cage = cage;
cages.Add(cage);
success = true;
}
}
}
}
}
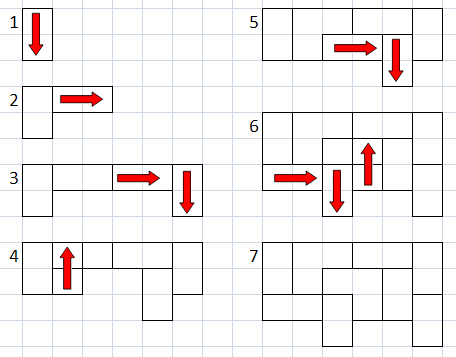
从板上的{0,0}位置开始,向右和向下移动,此功能将两个单元的块沿随机方向放置,并测试是否与现有笼子发生冲突.在这种情况下,笼子将合并;否则,将创建一个新的笼:(Starting from the {0,0} position on the board, and moving to the right and down directions, this function places pieces of two cells in random directions, and tests whether there is a conflict with an existent cage. In this case, the cages are merged; otherwise, a new cage is created:)
之后,(After that, the) PickOperation() 方法使用笼中的数字选择可能的随机运算(在+,-,x和÷之间选择).(method chooses a possible random operation (picked between +, -, x, and ÷) using the numbers inside the cage.)
public void PickOperation(Cage cage)
{
bool success = false;
while (!success)
{
if (currentOperation == 5)
currentOperation = 1;
switch (currentOperation)
{
case 1:
cage.Operation = Operations.Plus;
int sum = 0;
foreach (Cell cell in cage.CellList)
{
sum += Convert.ToInt32(cell.CellValue);
}
cage.Result = sum;
success = true;
break;
case 2:
cage.Operation = Operations.Minus;
if (cage.CellList.Count == 2)
{
int sub = Convert.ToInt32(cage.CellList[0].CellValue) -
Convert.ToInt32(cage.CellList[1].CellValue);
if (sub > 0)
{
cage.Result = sub;
success = true;
}
else
{
sub = Convert.ToInt32(cage.CellList[1].CellValue) -
Convert.ToInt32(cage.CellList[0].CellValue);
if (sub > 0)
{
cage.Result = sub;
success = true;
}
}
}
break;
case 3:
cage.Operation = Operations.Multiply;
int mult = 1;
foreach (Cell cell in cage.CellList)
{
mult *= Convert.ToInt32(cell.CellValue);
}
cage.Result = mult;
success = true;
break;
case 4:
cage.Operation = Operations.Divide;
if (cage.CellList.Count == 2)
{
int quo = Convert.ToInt32(cage.CellList[0].CellValue) /
Convert.ToInt32(cage.CellList[1].CellValue);
int rem = Convert.ToInt32(cage.CellList[0].CellValue) - quo *
Convert.ToInt32(cage.CellList[1].CellValue);
if (rem == 0)
{
cage.Result = quo;
success = true;
}
else
{
quo = Convert.ToInt32(cage.CellList[1].CellValue) /
Convert.ToInt32(cage.CellList[0].CellValue);
rem = Convert.ToInt32(cage.CellList[1].CellValue) - quo *
Convert.ToInt32(cage.CellList[0].CellValue);
if (rem == 0)
{
cage.Result = quo;
success = true;
}
}
}
break;
}
currentOperation++;
}
}
变得更聪明:和候选人一起玩(Getting Smarter: Playing With Candidates)
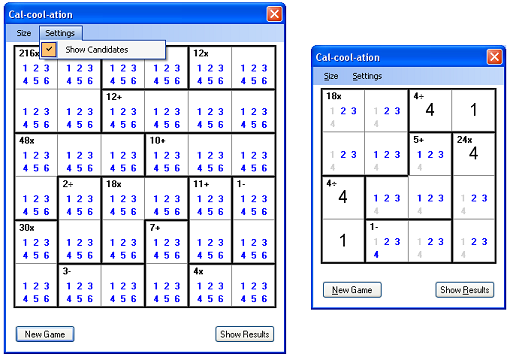
我必须承认,我觉得这个游戏对我来说很难.我可以面对3 x 3的面板,但是从4 x 4开始,事情变得更加复杂.如果我在纸上玩过这个游戏,我可能会记下哪些数字可以或不能放在单元格中.然后,我找到了某个单元格的正确数字,然后拿起铅笔穿过同一行和同一列中其他单元格中的该数字.然后我有了一个奇怪的想法:如果我允许用户直接在应用程序中做笔记怎么办?这就是通过菜单”(I must confess that I found this game difficult for me. I can face a 3 x 3 board, but from 4 x 4 on, things get more complicated. If I had this game on paper, I would probably take notes about which numbers can or can’t be placed in cells. Then I discovered the correct digit for a certain cell, I’d pick up my pencil to strike through that digit in the other cells in the same row and the same column. Then I had this weird idea: what if I allowed users to take notes directly in the application? And here it is, this new feature through the menu “)设定值(Settings)->(->)显示候选人(Show Candidates)",您可以在其中打开/关闭候选数字:(”, where you can turn on/off the candidate digits:)
请注意,当您与候选人一起玩时,界面会发生一些变化:(Notice that when you play with candidates, the interface changes a little bit:)
裸对(The Naked Pairs)
在获取一个单元格的随机数之前,您应该始终寻找"裸对".裸对表示在某行或某列中,有两个具有两个可能值的单元格.在下图中,我们可以发现这些裸对,只有两个可能的值[3,4]:(Before getting a random number for a cell, you should always look for “naked pairs”. Naked pairs mean that in some row or column, there are two cells with two possible values. In the figure below, we can spot these naked pairs, with only two possible values [3,4]:)
发现裸对的原因很简单:由于这两个单元格只能容纳这两位数字,因此该行中的其他任何单元格都不会包含"(The reason for spotting naked pairs is simple: since these two cells can hold only these two digits, no other cells in that row will have “) 3 " 要么 “(” or “) 4 “.因此,我们可以将它们从可能的数字中删除:(”. Thus we can remove them from the possible digits:)
兴趣点(Points of Interest)
我认为对我来说更难的部分是发现如何将数字随机排列在有效的N x N面板中(也就是说,不要在行和列中重复数字).经过研究,我发现了我之前提到的裸对/裸三胞胎技术.当然,我可以使用更多的技术,因此,如果您对它们感兴趣,不仅是作为开发人员,还是作为播放器,都可以使用:(I think the harder part for me was to discover how to randomly arrange the numbers in a valid N x N board (that is, without repeating digits in rows and columns). After some research, I found the naked pairs / naked triplets technique I mentioned before. Of course, there are many more techniques I could have used, so if you are interested in them, not only as a developer, but also as a player, here it goes:)
- 如何解决数独难题:视频系列(How to Solve Sudoku Puzzles: Video Series)
- 解决数独的技巧(Techniques For Solving Sudoku)
- 可以使用数独技巧吗?(Can You Use Some Sudoku Tips?)
历史(History)
- 2009-07-26(2009-07-26):第一篇文章(: First post)
- 2009-07-29(2009-07-29):新功能:“显示候选人”(: New feature: “Show Candidates”)
- 2009-07-30(2009-07-30):Visual Studio 2005的新版本(: New version for Visual Studio 2005)
许可
本文以及所有相关的源代码和文件均已获得The Code Project Open License (CPOL)的许可。
C# C#3.0 Win2003 Vista .NET3.5 Windows WinXP Dev 新闻 翻译