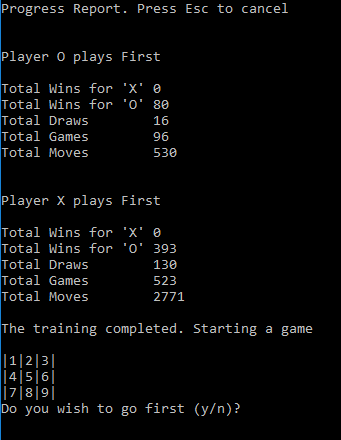
[译]强化学习-井字游戏示例
By robot-v1.0
本文链接 https://www.kyfws.com/ai/reinforcement-learning-a-tic-tac-toe-example-zh/
版权声明 本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
- 18 分钟阅读 - 9018 个词 阅读量 0强化学习-井字游戏示例(译文)
原文地址:https://www.codeproject.com/Articles/1400011/Reinforcement-Learning-A-Tic-Tac-Toe-Example
原文作者:George Swan
译文由本站 robot-v1.0 翻译
前言
An example of how the temporal difference algorithm can be used to teach a machine to become invincible at Tic Tac Toe in under a minute
如何使用时差算法教机器在一分钟内在井字游戏中立于不败之地的示例
介绍(Introduction)
强化学习是一步一步的机器学习过程,在每一步之后,机器都会收到奖励,该奖励反映了该步骤在实现目标方面的优劣.通过探索其环境并利用最有意义的步骤,它学会了在每个阶段选择最佳行动.(Reinforcement Learning is a step by step machine learning process where, after each step, the machine receives a reward that reflects how good or bad the step was in terms of achieving the target goal. By exploring its environment and exploiting the most rewarding steps, it learns to choose the best action at each stage.)
井字游戏示例(Tic Tac Toe Example)
这件作品的重点是教人工智能玩井字游戏,或更准确地说,是在井字游戏中获胜.实际上,它对游戏规则一无所知,也不存储所进行动作的历史.在每个回合中,它仅从可用动作中选择具有最高潜在奖励的动作.这些动作的相对价值是在训练期间通过对模拟游戏中获得的动作和奖励进行采样来学习的.在深入探讨如何实现此目的之前,弄清楚强化学习中使用的一些术语可能会有所帮助.(This piece is centred on teaching an artificial intelligence to play Tic Tac Toe or, more precisely, to win at Tic Tac Toe. It doesn’t actually know anything about the rules of the game or store the history of the moves made. On each turn, it simply selects a move with the highest potential reward from the moves available. The relative merit of these moves is learned during training by sampling the moves and rewards received during simulated games. Before diving into how this is achieved, it may be helpful to clarify some of the nomenclature used in reinforcement learning.)
强化学习术语(Reinforcement Learning Terminology)
人工智能被称为(The artificial intelligence is known as the)代理商(Agent).在每个步骤中,(. At each step, it performs an)**行动(Action)**这导致了一些变化(which results in some change in the)**州(state)**的(of the)**环境(Environment)**它在其中运作.环境通过根据行为的优劣来奖励Agent以做出响应.然后,环境向代理提供反馈,以反映环境的新状态并使代理具有足够的信息来采取下一步措施.代理遵循(in which it operates. The environment responds by rewarding the Agent depending upon how good or bad the action was. The environment then provides feedback to the Agent that reflects the new state of the environment and enables the agent to have sufficient information to take its next step. The Agent follows a)**政策(policy)**确定从给定状态采取的操作.学习过程改善了政策.因此,实际上是在构建策略,而不是代理.代理是策略的代理,执行策略规定的操作.每个州都有从该州获得的预期回报的价值(以报酬的形式).状态的值用于在状态之间进行选择.该政策通常是一种贪婪的政策.也就是说,选择具有最高价值的状态,作为强化学习的基本前提是,在每个步骤中都能获得最高预期奖励的策略是遵循的最佳策略.为了使该决策过程有效,该过程必须是(that determines the action it takes from a given state. The learning process improves the policy. So it’s the policy that is actually being built, not the agent. The agent is the agent of the policy, taking actions dictated by the policy. Each state has the value of the expected return, in terms of rewards, from being in that state. A state’s value is used to choose between states. The policy is usually a greedy one. That is, the state with the highest value is chosen, as a basic premise of reinforcement learning is that the policy that returns the highest expected reward at every step is the best policy to follow. For this decision process to work, the process must be a) 马尔可夫决策过程.(Markov Decision Process.)
马尔可夫决策过程(Markov Decision Process)
马尔可夫决策过程(MDP)是一步一步的过程,其中当前状态具有足够的信息以能够确定处于每个后续状态的概率.为了更好地理解MDP,有时最好考虑什么过程不是MDP.如果您试图绘制给定时间步长上的汽车位置,并且没有得到汽车的方向,而是获得了速度,那将不是MDP,因为汽车在每个时间步长上所处的位置(状态)无法确定.另一个示例是一个过程,其中每个步骤的操作是从一叠纸牌中抽出一张纸牌,如果是面卡则向左移动,如果不是一张面卡则向右移动.在这种情况下,可能的状态是已知的,要么是左侧的状态,要么是右侧的状态,但是由于处于堆栈中的牌分布是未知的,因此不知道处于任一状态的可能性,因此不是一个MDP.(A Markov decision process (MDP) is a step by step process where the present state has sufficient information to be able to determine the probability of being in each of the subsequent states. To get a better understanding of an MDP, it is sometimes best to consider what process is not an MDP. If you were trying to plot the position of a car at a given time step and you were given the direction but not the velocity of the car, that would not be a MDP as the position (state) the car was in at each time step could not be determined. Another example is a process where, at each step, the action is to draw a card from a stack of cards and to move left if it was a face card and to move right if it wasn’t. In this case, the possible states are known, either the state to the left or the state to the right, but the probability of being in either state is not known as the distribution of cards in the stack is unknown, so it isn’t an MDP.)
将Tic Tac Toe作为Markov决策过程实施(Implementing Tic Tac Toe as a Markov Decision Process)
井字游戏非常容易实现为马尔可夫决策过程,因为每一步动作都是一个改变动作状态的步骤.代理在每个步骤可使用的操作数等于面板3X3网格上未占用的方块数.代理需要能够根据预期奖励来查找由每个可用操作产生的状态的值,然后选择具有最高值的操作.当代理商对许多举动进行采样以及由于举动而获得的报酬时,它会在训练期间学习状态和动作的价值.作为训练过程的一部分,记录状态值已更新的次数,因为每次更新都会减少值的更新量.因此,每个状态都需要有一个唯一的键,该键可用于查找该状态的值以及该状态已更新的次数.如果播放状态可以加密为数值,则可以将其用作字典的密钥,该字典既可以存储状态更新的次数,又可以将状态值存储为(Tic Tac Toe is quite easy to implement as a Markov Decision process as each move is a step with an action that changes the state of play. The number of actions available to the agent at each step is equal to the number of unoccupied squares on the board’s 3X3 grid. The agent needs to be able to look up the values, in terms of expected rewards, of the states that result from each of the available actions and then choose the action with the highest value. The agent learns the value of the states and actions during training when it samples many moves along with the rewards that it receives as a result of the moves. As part of the training process, a record is kept of the number of times that a state’s value has been updated because the amount by which the value is updated is reduced with each update. So each state needs to have a unique key that can be used to lookup the value of that state and the number of times the state has been updated. If the state of play can be encrypted as a numeric value, it can be used as the key to a dictionary that stores both the number of times the state has been updated and the value of the state as a) ValueTuple 类型(of type) int,double .这样做的明显方法是将状态编码为一个可能的九位数正整数,使" X"的值为2,而" O"的值为1.因此,下面的游戏状态将被编码为(. The obvious way to do this is to encode the state as a, potentially, nine figure positive integer giving an ‘X’ a value of 2 and a ‘O’ a value of 1. So the state of play below would be encoded as) 200012101 .(.)
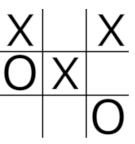 平方中的" X"值等于2乘以10乘以平方的指数值(0-8)的幂,但是使用以3为底的方法比以10为底的方法更有效.记号,板编码为:(The value of an ‘X’ in a square is equal to 2 multipled by 10 to the power of the index value (0-8) of the square but it’s more efficient to use base 3 rather than base 10 so, using the base 3 notation,, the board is encoded as:)
平方中的" X"值等于2乘以10乘以平方的指数值(0-8)的幂,但是使用以3为底的方法比以10为底的方法更有效.记号,板编码为:(The value of an ‘X’ in a square is equal to 2 multipled by 10 to the power of the index value (0-8) of the square but it’s more efficient to use base 3 rather than base 10 so, using the base 3 notation,, the board is encoded as:)
(1*3^0)+(1*3^2)+(2*3^3)+(1*3^4)+(2*3^8)=13267
用于将板阵列加密为基数为3的方法非常简单.(The method for encrypting the board array into a base 3 number is quite straight forward.)
public int BoardToState()
{
int id = 0;
for (int i = 0; i < Squares.Length; i++)
{
int value = 0;
if (!Squares[i].IsEmpty)
{
value = Squares[i].Content == 'X' ? 1 : 2;
id += (int)(value * Math.Pow(3, Squares[i].BoardIndex));
}
}
return id;
}
解密方法如下:(The decrypt method is as follows:)
public IBoard StateToBoard(int s)
{
int state = s;
var board = new OXBoard();
for (int i = board.Squares.Length-1; i >=0; i--)
{
int value =(int)(state/ Math.Pow(3, i));
if(value!=0)
{
board[i].Content = value == 1 ? 'X' : 'O';
state -= (int)(value * Math.Pow(3, i));
}
}
return board;
}
的(The) StateToStatePrimes 下面的方法迭代空缺的正方形,并在每次迭代中选择如果代理要占据那个正方形将产生的新状态.所选状态作为数组返回,代理可以从中选择具有最高值的状态并进行移动.(method below iterates over the vacant squares and, with each iteration, selects the new state that would result if the agent was to occupy that square. The selected states are returned as an array from which the agent can select the state with the highest value and make its move.)
public int[] StateToStatePrimes(int state)
{
int existingState = state;
List<int> statePrimes = new List<int>();
for (int i = 8; i >= 0; i--)
{
int value = (int)(state / Math.Pow(3, i));
if (value == 0)
{
//agent is'O'
var sPrime = existingState + (int)(2 * Math.Pow(3, i));
statePrimes.Add(sPrime);
}
state -= (int)(value * Math.Pow(3, i));
}
return statePrimes.ToArray();
}
使用这些方法后,接下来要考虑的是如何学习一种策略,在该策略中,分配给状态的值是准确的,所采取的行动是制胜法宝.这是(With these methods in place, the next thing to consider is how to learn a policy where the values assigned to states are accurate and the actions taken are winning ones. This is where the) 贝尔曼方程(Bellman Equation) 发挥作用.(comes into play.)
贝尔曼方程(The Bellman Equation)
强化学习围绕贝尔曼方程式进行.该等式将处于当前状态的值与通过在每个后续步骤中采取措施而获得的预期收益相关联.它由两部分组成:采取行动的奖励和下一个状态的折现值.(Reinforcement learning is centred around the Bellman equation. The equation relates the value of being in the present state to the expected reward from taking an action at each of the subsequent steps. It consists of two parts, the reward for taking the action and the discounted value of the next state.)
v(s1) = R + γ*v(s2)
其中v(s1)是当前状态的值,R是采取下一个动作的奖励,而γ* v(s2)是下一个状态的折现值.伽玛(γ)是折扣因子.它的使用导致即时奖励比将来的奖励更重要.折扣因子在持续的流程中特别有用,因为它可以防止不断循环的回馈. Bellman方程在每个步骤中都使用,并且以类似递归的方式应用,以使在执行下一步骤时,下一个状态的值变为当前状态的值.因此,确定打开状态值的问题被分解为在到达终点运动的整个过程中采用一系列步骤应用Bellman方程.实际上,从终止游戏的动作开始进行倒退工作更容易思考.那是在(*Where v(s1) is the value of the present state, R is the reward for taking the next action and γ*v(s2) is the discounted value of the next state. Gamma (γ) is the discount factor. Its use results in immediate rewards being more important than future rewards. The discount factor is particularly useful in continuing processes as it prevents endless loops from racheting up rewards. The Bellman equation is used at each step and is applied in recursive-like way so that the value of the next state becomes the value of the current state when the next steps taken. So the problem of determining the values of the opening states is broken down into applying the Bellman equation in a series of steps all the way to the end move. Actually, it’s easier to think in terms of working backwards starting from the move that terminates the game. That is the approach used in*) 动态编程(Dynamic programming) .(*.*)
动态编程(Dynamic Programming)
动态编程与C#编程不同.通过将其分解为一系列步骤,可以解决数学问题.通过重复应用Bellman方程,可以通过从每个可能的最终状态(最后移动)一直到第一状态(打开移动)反向(备份)来确定井字游戏中每个可能状态的值.要了解其工作原理,请考虑以下示例.(Dynamic Programming is not like C# programming. It is a way of solving a mathematical problem by breaking it down into a series of steps. By repeatedly applying the Bellman equation, the value of every possible state in Tic Tac Toe can be determined by working backwards (backing up) from each of the possible end states (last moves) all the way to the first states (opening moves). To get an idea of how this works, consider the following example.)
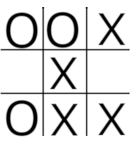 奖励系统设置为11赢,平局6.中介,(The reward system is set as 11 for a win, 6 for a draw. The agent,)
奖励系统设置为11赢,平局6.中介,(The reward system is set as 11 for a win, 6 for a draw. The agent,) playerO ,处于状态10304,可以选择2个动作,进入方格3,这将导致状态10304 + 2 * 3 ^ 3 =10358的转换,并获得11的奖励赢得游戏或进入方格5,这将导致状态10304 + 2 * 3 ^ 5 =10790的过渡,在这种情况下,游戏为平局,代理商会获得6的奖励.策略选择了最高奖励的状态,因此代理商进入了三等奖和胜利.根据此经验,代理可以获取一条重要的信息,即处于状态10304的值.从该状态,代理可以平等地选择进入状态10358并获得11的奖励或进入状态10790并获得收到6的奖励,因此处于状态10304的值为(11 + 6)/2=8.5.状态10358和10780被称为终端状态,其值为零,因为状态的值被定义为从期望状态开始,处于该状态并遵循代理程序策略的值.通过考虑所有可能的结束运动并不断地将状态值从当前状态备份到可用于前一运动的所有状态,可以确定所有相关值,直到回到开始运动为止.这在像井字游戏这样的简单游戏中是可行的,但在大多数情况下在计算上过于昂贵.一种更实用的方法是使用(, is in state 10304, it has a choice of 2 actions, to move into square 3 which will result in a transition to state 10304 + 23^3=10358 and win the game with a reward of 11 or to move into square 5 which will result in a transition to state 10304 + 23^5=10790 in which case the game is a draw and the agent receives a reward of 6. The policy selects the state with the highest reward and so the agent moves into square 3 and wins. From this experience, the agent can gain an important piece of information, namely the value of being in the state 10304. From this state, it has an equal choice of moving to state 10358 and receiving a reward of 11 or moving to state 10790 and receiving a reward of 6 So the value of being in state 10304 is (11+6)/2=8.5. States 10358 and 10780 are known as terminal states and have a value of zero because a state’s value is defined as the value, in terms of expected returns, from being in the state and following the agent’s policy from then onwards. By considering all possible end moves and continually backing up state values from the current state to all of the states that were available for the previous move, it is possible to determine all of the relevant values right the way back to the opening move. This is feasible in a simple game like tic tac toe but is too computationally expensive in most situations. A more practical approach is to use) 蒙特卡洛评估.(Monte Carlo evaluation.)
蒙特卡洛评估(Monte Carlo Evaluation)
蒙特卡洛评估通过重复采样MDP的完整情节并确定在许多情节中遇到的每个状态的平均值,简化了确定MDP中每个状态的值的问题.在井字游戏中,情节是一个完整的游戏.如果在第一集中,结果是获胜,奖励值为10,则游戏中遇到的每个状态的值将为10.在第二集中,结果是平局,奖励为6. ,则游戏中遇到的每个状态都将被赋予6的值,除了第一个游戏中也遇到的状态.这些状态现在将具有(10 + 6)/2 =8的值.在许多事件中,国家的价值将非常接近其真实价值.由于MDP很短,因此该技术将非常适合井字游戏.但是,当它与更复杂的MDP一起部署时,会出现一些问题.状态值需要很长时间才能收敛到其真实值,并且每个情节都必须终止才能进行任何学习.还可以使用其他技术来确定避免这些问题的最佳策略,其中一项众所周知的方法是时间差异学习.(Monte Carlo evaluation simplifies the problem of determining the value of every state in a MDP by repeatedly sampling complete episodes of the MDP and determining the mean value of every state encountered over many episodes. In Tic Tac Toe, an episode is a single completed game. If, in the first episode, the result was a win and the reward value was 10, every state encountered in the game would be given a value of 10. If, in the second episode, the result was a draw and the reward was 6, every state encountered in the game would be given a value of 6 except for the states that were also encountered in the first game. These states would now have value of (10+6)/2=8. Over many episodes, the value of the states will become very close to their true value. This technique will work well for games of Tic Tac Toe because the MDP is short. There are, however, a couple of issues that arise when it is deployed with more complicated MDPs. The state values take a long time to converge to their true value and every episode has to terminate before any learning can take place. There are other techniques available for determining the best policy that avoid these problems, a well known one is Temporal Difference Learning.)
时间差异学习(Temporal Difference Learning)
时间差异学习是一种算法,其中通过重复采样从一个状态到另一个状态的转换来改进选择每个步骤要采取的动作的策略.通过采用一种称为自举的机制来更新状态值,与蒙特卡洛评估相比,它具有更高的性能.通过使用下一个状态的值上拉(或下拉)现有状态的值来实现自举.因为这只是向前看的第一步,所以可以在MDP实际运行时使用它,而无需等待进程终止.学习过程涉及使用在状态中执行的操作的值来更新该状态的值.一个州的价值在形式上被定义为:根据预期收益,从处于该州开始并遵循代理的策略的价值.行动值是指按照预期的奖励采取行动并从那时起遵循代理人的政策的值.为了从动作值更新状态值,需要知道动作转换到下一状态的概率.它并非总是100%,因为某些动作具有随机成分.但是,如果存储了操作值而不是状态值,则可以通过对操作值到操作值之间的步骤进行采样来简单地更新它们的值,方法类似于蒙特卡洛评估,并且代理不需要具有转移概率模型.使用动作值而不是状态值的时间差异学习称为Q学习(Q值是动作值的另一个名称). Bellman方程用于更新动作值.(Temporal difference learning is an algorithm where the policy for choosing the action to be taken at each step is improved by repeatedly sampling transitions from state to state. It achieves superior performance over Monte Carlo evaluation by employing a mechanism known as bootstrapping to update the state values. Bootstrapping is achieved by using the value of the next state to pull up (or down) the value of the existing state. As it’s a one step look ahead, it can be used while the MDP is actually running and does not need to wait until the process terminates. The learning process involves using the value of an action taken in a state to update that state’s value. A state’s value is formally defined as the value, in terms of expected returns, from being in the state and following the agent’s policy from then onwards. The action value is the value, in terms of expected rewards, for taking the action and following the agent’s policy from then onwards. In order to update a state value from an action value, the probability of the action resulting in a transition to the next state needs to be known. It is not always 100% as some actions have a random component. But, if action values are stored instead of state values, their values can simply be updated by sampling the steps from action value to action value in a similar way to Monte Carlo Evaluation and the agent does not need to have a model of the transition probabilities. Temporal Difference Learning that uses action values instead of state values is known as Q-Learning, (Q-value is another name for an action value). The Bellman equation is used to update the action values.)
currentStateVal = currentStateVal + alpha * (-1 + (gamma*newStateVal) - currentStateVal);
当前状态的Q值更新为当前状态的Q值加上下一个状态的Q值减去当前状态的值减去因子" alpha".下一个状态的值包括进入该状态的奖励(-1).变量alpha是应用于两个状态之间差异的折扣因子.状态更新得越多,更新量就变得越小. Alpha只是1/N,其中N是状态已更新的次数.如前所述,γ是用于折现未来奖励的折现因子. Epsilon贪婪策略用于选择操作.(The Q-value of the present state is updated to the Q-value of the present state plus the Q-value of the next state minus the value of the present state discounted by a factor, ‘alpha’. The value of the next state includes the reward (-1) for moving into that state. The variable, alpha, is a discount factor that’s applied to the difference between the two states. The more the state is updated the smaller the update amount becomes. Alpha is simply 1/N where N is the number of times the state has been updated. As previously mentioned, γ is a discount factor that’s used to discount future rewards. An Epsilon greedy policy is used to choose the action.)
Epsilon贪婪政策改进(Epsilon Greedy Policy Improvement)
贪婪策略是一种在每个时间步选择具有最高Q值的操作的策略.如果将其应用于每个步骤,那么将通过MDP过度利用现有途径,而对新途径的探索将不足.因此,在每个步骤中,以ε百分比的频率进行随机选择,并以1ε百分比的频率选择贪婪策略.在简短的MDP中,最好将epsilon设置为较高的百分比.在广泛的MDP中,ε可以设置为较高的初始值,然后随时间减小.(A greedy policy is a policy that selects the action with the highest Q-value at each time step. If this was applied at every step, there would be too much exploitation of existing pathways through the MDP and insufficient exploration of new pathways. So, at each step, a random selection is made with a frequency of epsilon percent and a greedy policy is selected with a frequency of 1-epsilon percent. In a short MDP, epsilon is best set to a high percentage. In an extensive MDP, epsilon can be set to a high initial value and then be reduced over time.)
学习方法(The Learning Method)
每个状态需要存储两个值,即状态值和该值被更新的次数.一种(Two values need to be stored for each state, the value of the state and the number of times the value has been updated. A) Dictionary 用于存储所需的数据.它使用编码为整数的状态作为键和(is used to store the required data. It uses the state, encoded as an integer, as the key and a) ValueTuple 类型(of type) int, double 作为价值.键引用状态和(as the value. The key references the state and the) ValueTuple 存储更新次数和状态值.(stores the number of updates and the state’s value.)
public Dictionary<int, (int, double)> FitnessDict { get; private set; }
//.....
public void Learn(int[] states, GameState gameState)
{
double gamma = Constants.Gamma;
int currState = states[0];
int newState = states[1];
UpdateFitnessDict(newState, gameState);//add if not present
(int currStateCount, double currStateVal) = FitnessDict[currState];
currStateCount += 1;
double alpha = 1 / (double)currStateCount;
(int newStateCount, double newStateVal) = FitnessDict[newState];
if (gameState != GameState.InPlay)
{
currStateVal = currStateVal + (alpha * (rewardsDict[gameState] - currStateVal));
FitnessDict[currState] = (currStateCount, currStateVal);
return;
}
currStateVal = currStateVal + alpha * (-1 + (gamma*newStateVal) - currStateVal);
FitnessDict[currState] = (currStateCount, currStateVal);
}
private void UpdateFitnessDict(int newState, GameState gameState)
{
if (!FitnessDict.ContainsKey(newState))
{
FitnessDict.Add(newState, (0, rewardsDict[gameState]));
}
}
训练(Training)
训练包括从状态到状态重复采样动作,并在每个动作之后调用学习方法.在训练期间,游戏中的每一步动作都是MDP的一部分.在坐席人员的行动中,坐席人员可以选择行动,除非仅剩一个空缺方格.当是对手的移动时,座席将进入对手选择的状态.这种安排使代理能从自己的选择和对手的反应中学习.它还封装了状态的每一个变化.训练需要包括代理首先打的游戏和对手首先打的游戏.训练方法异步运行,并可以报告进度和取消进度.(Training consists of repeatedly sampling the actions from state to state and calling the learning method after each action. During training, every move made in a game is part of the MDP. On the agent’s move, the agent has a choice of actions, unless there is just one vacant square left. When it’s the opponent’s move, the agent moves into a state selected by the opponent. This arrangement enables the agent to learn from both its own choice and from the response of the opponent. It also encapsulates every change of state. Training needs to include games where the agent plays first and games where the opponent plays first. The training method runs asynchronously and enables progress reporting and cancellation.)
public void Train(int max, bool isOFirst, IProgress<int> progress, CancellationToken ct)
{
int maxGames = max;
int[] states = new int[2];
char[] Players = isOFirst ? new char[] { 'O', 'X' } : new char[] { 'X', 'O' };
int totalMoves = 0;
int totalGames = 0;
Move move;
while (totalGames < maxGames)
{
move.MoveResult = GameState.InPlay;
move.Index = -1;
int moveNumber = 0;
int currentState = 0;
int newState = 0;
board.Reset();
while (move.MoveResult == GameState.InPlay)
{
char player = Players[moveNumber % 2];
move = player == 'X' ? RandMoveX() : RandMoveO(currentState);
board[move.Index].Content = player;
newState = board.BoardToState();
if (move.MoveResult == GameState.InPlay
&& !board.Lines.Any(l => !l.IsLineOblocked || !l.IsLineXblocked))
{
move.MoveResult = GameState.Draw;
}
states[0] = currentState;
states[1] = newState;
learner.Learn(states, move.MoveResult);
currentState = newState;
moveNumber++;
}
totalMoves += moveNumber - 1;
totalGames += 1;
if(totalGames % Constants.ReportingFreq == 0)
{
progress.Report(totalGames / maxGames);
ct.ThrowIfCancellationRequested();
}
}
}
可靠测试(Infallibility Testing)
培训周期包括两个部分.在第一部分中,特工扮演开幕式.在第二部分中,对手开始游戏.在每个部分之后,都会针对对手的所有可能下注对策略进行测试.如果找不到对手的获胜者,则训练将停止,否则将重复该循环.在我的机器上,完成培训通常不到一分钟.测试方法的详细信息以及确定各种比赛状态的方法已在较早的时候给出.(A training cycle consists of two parts. In the first part, the agent plays the opening moves. In the second part, the opponent starts the games. After every part, the policy is tested against all possible plays by the opponent. When no win is found for the opponent, training stops, otherwise the cycle is repeated. On my machine, it usually takes less than a minute for training to complete. Details of the testing method and the methods for determining the various states of play are given in an earlier) 文章(article) 在那里开发了基于策略的井字游戏解决方案.(where a strategy based solution to playing tic tac toe was developed.)
private Progress<int> progress = new Progress<int>();
private CancellationTokenSource cts = new CancellationTokenSource();
private IRandomTrainer trainer;
private IInfallibilityTester tester;
public TrainingScheduler(IRandomTrainer trainer, IInfallibilityTester tester)
{
this.tester = tester;
this.trainer = trainer;
progress.ProgressChanged += ReportProgress;
}
private void ReportProgress(object sender, int percent)
{
if (Console.KeyAvailable && Console.ReadKey(true).Key == ConsoleKey.Escape)
{
Console.Write(Constants.Cancelling);
cts.Cancel();
}
Console.Write(".");
}
public async Task ScheduleTraining()
{
int runsX = Constants.TrainingRunsX;
int runsO = Constants.TrainingRunsO;
int xFirstResult = -1;
int oFirstResult = -1;
bool isPlayerOFirst = true;
Console.WriteLine(Constants.TrainingPressEsc);
int iterations = 0;
while (xFirstResult != 0 || oFirstResult != 0)//number of'X' wins
{
if (iterations == Constants.IterationsBeforeReset)
{
iterations = 0;
//Resetting the state values and visit counts is not essential
//But it improves efficiency where convergence is slow.
trainer.Reset();
}
try
{
await Task.Run(() => trainer.Train(runsO, isPlayerOFirst, progress, cts.Token));
await Task.Run(() => trainer.Train(runsX, !isPlayerOFirst, progress, cts.Token));
oFirstResult = tester.RunTester(isPlayerOFirst);
xFirstResult = tester.RunTester(!isPlayerOFirst);
iterations += 1;
}
catch (OperationCanceledException)
{
throw;
}
}
}
设置奖励值(Setting The Reward Values)
使代理程序中的MDP中的每个步骤都很痛苦,这一点很重要,这样它才能采用最快的路线.值为-1效果很好,并构成其他奖励的基线.获胜的奖励与平局的奖励之间必须存在正差,否则代理将选择慢速获胜而不是快速获胜.确切值并不重要.当状态值之间的差异较小时,状态值似乎会更快收敛到其真实值.(It’s important to make each step in the MDP painful for the agent so that it takes the quickest route. A value of -1 works well and forms a base line for the other rewards. There needs to be a positive difference between the reward for a Win and the reward for a Draw or else the Agent will choose a quick Draw over a slow win. The exact values are not critical. It would appear that the state values converge to their true value more quickly when there is a relatively small difference between the) Win(10) ,(,) Draw(2) 和(and) Lose(-30) ,大概是因为时间差异学习引导了状态值,并且如果差异很小,那么繁琐的工作就更少了.括号中的数字是示例应用程序中使用的值,此外,折扣值" gamma"设置为0.9.毫无疑问,只要稍微调整一下这些数字,性能就可以进一步提高.(, presumably because temporal difference learning bootstraps the state values and there is less heavy lifting to do if the differences are small. The figures in brackets are the values used in the example app, in addition, the discount value ‘gamma’ is set at 0.9. No doubt performance can be improved further if these figures are ‘tweaked’ a bit.)
结论(Conclusion)
强化学习是一种非常强大的算法,它使用一系列相对简单的步骤链接在一起,以产生一种人工智能形式.但是,在强化学习中使用的术语以及应用Bellman方程的半递归方式可能会使新手难以理解该主题.希望这个过于简化的文章可以在一定程度上消除该主题的神秘性,并鼓励对该主题进行进一步的研究.(Reinforcement learning is an amazingly powerful algorithm that uses a series of relatively simple steps chained together to produce a form of artificial intelligence. But the nomenclature used in reinforcement learning along with the semi recursive way the Bellman equation is applied can make the subject difficult for the newcomer to understand. It’s hoped that this oversimplified piece may demystify the subject to some extent and encourage further study of this fascinating subject.)
参考和致谢(References and Acknowledgements)
- Tom M. Mitchell的机器学习.机器学习概述,其中有关于强化学习的出色章节.(Machine Learning by Tom M. Mitchell. An overview of machine learning with an excellent chapter on Reinforcement Learning.)
- 强化学习:Richard S. Sutton和Andrew G. Barto的简介.这是强化学习的预言,但对于初学者而言,学习曲线非常陡峭.草案版本可在线获得,但现在可能受版权保护.(Reinforcement Learning: An Introduction by Richard S. Sutton and Andrew G. Barto. This is the oracle of reinforcement learning but the learning curve is very steep for the beginner. A draft version was available online but may now be subject to copyright.)
- David Silver的强化学习课程.一系列非常有启发性的讲座,虽然假定您不了解该主题,但对数学符号有所了解会有所帮助.在线可用费用(Reinforcement Learning Course by David Silver. A very informative series of lectures that assumes no knowledge of the subject but some understanding of mathematical notations is helpful. Available fee online) 这里(here)
- TicTacToe-没有递归的MiniMax(TicTacToe - MiniMax Without Recursion) 由肯尼迪(Chris Kennedy)撰写.井字游戏的一个有趣的蛮力实现,很好地解释了如何将比赛状态编码为正3基整数.(by Christ Kennedy. An interesting brute force implementation of Tic Tac Toe with a good explanation of how to encode states of play as a positive base 3 integer.)
许可
本文以及所有相关的源代码和文件均已获得The Code Project Open License (CPOL)的许可。
C# .NET Architect machine-learning 新闻 翻译